How to do clustering
Clustering
Clustering is a type of unsupervised learning that involves grouping similar inputs into clusters or categories.
This technique can be used to identify patterns or relationships in data that may not be immediately apparent. There are many algorithms that can be used for clustering, including k-means, hierarchical clustering, and DBSCAN. The choice of clustering algorithm depends on the specific problem and the characteristics of the data.
Hard clustering → Assigning each instance to a single cluster.
Soft clustering → Assigning each instance a score per cluster, it can be a similarity score (or affinity).
Types of Clustering
There are several types of clustering algorithms, including:
Centroid-based clustering
Centroid-based clustering is a type of clustering method in which the position of a cluster is represented by the central point of its objects.
A popular example of centroid-based clustering is the k-means algorithm. Centroid-based algorithms are efficient but sensitive to initial conditions and outliers.
Fig: Centroid based clustering
Let’s learn about K-means clustering, an example of centroid-based clustering.
K-Means
The model learns to group inputs into k clusters based on similarity. It is a straightforward and efficient algorithm for data segmentation and pattern recognition.
The main objective of k-means clustering is to partition the data into ‘k’ clusters, where ‘k’ is a user-defined parameter representing the number of clusters desired.
Here’s how the k-means clustering algorithm works:
- Initialization: Choose ‘k’ initial centroids (cluster centers) randomly from the data points. These centroids represent the initial cluster centers.
- Assignment: Assign each data point to the nearest centroid. This step is based on the distance metric, commonly the Euclidean distance, but other distance measures can also be used.
- Update Centroids: Calculate the mean of all the data points assigned to each centroid. Move the centroid to the mean position. This step aims to find the new cluster centers.
- Repeat Assignment and Update: Repeatedly assign data points to the nearest centroid and update the centroids until convergence or until a maximum number of iterations is reached.
- Convergence: The algorithm converges when the centroids no longer change significantly between iterations or when a predefined convergence criterion is met.
- Result: After convergence, each data point will be assigned to one of the ‘k’ clusters based on the final positions of the centroids.
When sets of circles from competing centroids overlap they form a line. The result is what’s called a Voronoi tessellation.
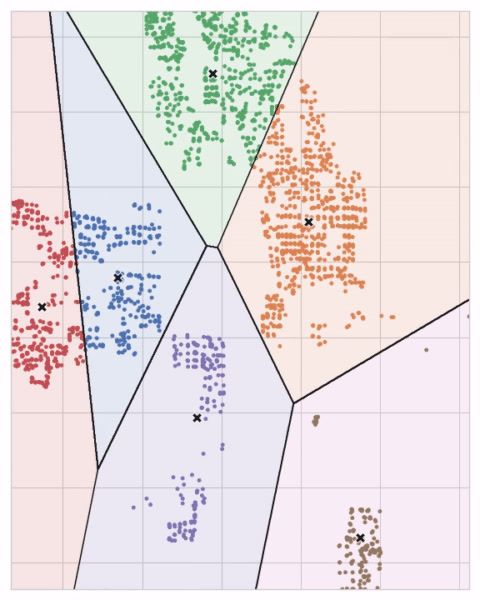
Fig: K-means clustering creates a Voronoi tessallation of the feature space.
Choosing the appropriate value of ‘k’ is critical in k-means clustering. The number of clusters should be determined based on domain knowledge or through techniques like the elbow method, silhouette score, or other clustering evaluation metrics.
K-means clustering is widely used in various applications, such as customer segmentation, image compression, anomaly detection, and data preprocessing for other machine learning tasks.
It is important to note that k-means is sensitive to the initial random centroid selection, and it may converge to a suboptimal solution depending on the initial positions of the centroids.
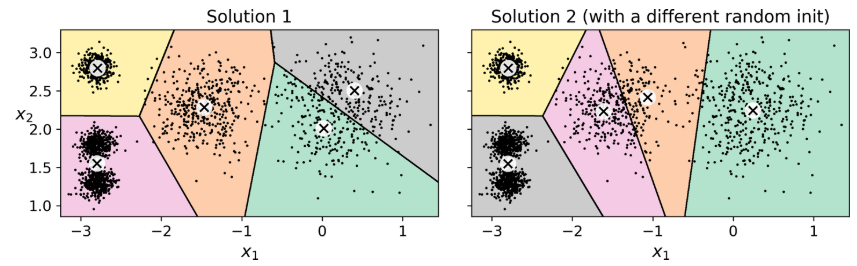
Fig: Suboptimal solutions due to unlucky centroid initializations
To mitigate this issue, it is common to run the algorithm multiple times with different initializations and choose the best result based on a chosen evaluation metric.
Disadvantages of K-means algorithm:
- Need to run K-means few times, before finding global optimal solution.
- Need to specify number of clusters.
- K-means does not behave very well when the clusters have varying sizes, different densities, or non-spherical shapes.
Let’s demonstrate the K-means clustering using a real-world dataset. Here, we’ll use the popular Iris dataset available in the sklearn datasets module. This dataset includes measurements of 150 iris flowers from three different species.
from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
# Load the iris dataset
iris = load_iris()
X = iris.data
# Apply K-means clustering
kmeans = KMeans(n_clusters=3, random_state=0, n_init=1) # n_init tells how many random initializations to do (times the whole process is repeated)
kmeans.fit(X)
labels = kmeans.labels_
# labels
"""
array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
1, 1, 1, 1, 1, 1, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 2, 2, 2, 2, 0, 2, 2, 2,
2, 2, 2, 0, 0, 2, 2, 2, 2, 0, 2, 0, 2, 0, 2, 2, 0, 0, 2, 2, 2, 2,
2, 0, 2, 2, 2, 2, 0, 2, 2, 2, 0, 2, 2, 2, 0, 2, 2, 0], dtype=int32)
"""
# Plot the clusters (plot using any 2 attributes, your wish)
plt.scatter(X[:, 2], X[:, 3], c=labels)
plt.scatter(kmeans.cluster_centers_[:, 2], kmeans.cluster_centers_[:, 3], s=300, c='red')
plt.show()
# Some other functions
y_pred = kmeans.fit_predict(X)
kmeans.transform(X) # score for each cluster

In this code, iris.data is a 150x4 matrix where each row is a flower sample and each column is a feature (sepal length, sepal width, petal length, petal width). The K-means algorithm groups the flowers into 3 clusters based on these features. The final line plots the clusters, with the cluster centers marked in red.
Density-based clustering
Density-based clustering connects areas of high example density into clusters. This method can form clusters of any shape as long as dense areas are connected. However, it struggles with data that has different densities and many dimensions. Also, these algorithms intentionally do not include outliers in any clusters.
Fig: Density based clustering
- DBSCAN Clustering: the model learns to group inputs into clusters based on density, with high-density regions representing clusters and low-density regions representing noise.
- Mean Shift Clustering: the model learns to identify and group inputs based on local density maxima.
Distribution-based clustering
This clustering approach assumes data is composed of distributions, such as Gaussian distributions. As distance from the distribution’s center increases, the probability that a point belongs to the distribution decreases.
Fig: Distribution-based clustering
A common example of distribution-based clustering is the Gaussian Mixture Model (GMM).
Hierarchical clustering
The model learns to group inputs into a hierarchy of clusters, with larger clusters containing smaller clusters.
Fig: Hierarchical clustering
- Agglomerative clustering
- BIRCH (scale well to large dataset)
Each type of clustering algorithm is suited for different types of data and problems, and choosing the right type of clustering is an important part of building an accurate machine learning model.
Applications of Clustering:
- Data analysis
- Customer segmentation
- recommender systems
- Dimensionality reduction
- Anomaly detection (outlier detection)
- Search engines
- image segmentation
- Semi-supervised learning
Creating a Similarity Matrix
A similarity matrix is a matrix where each element ij represents the similarity between the ith and jth elements of the dataset. A common method of calculating similarity is by using the Euclidean distance.
In the context of clustering, we use a similarity matrix to find the similarity between any element and it’s corresponding centroid.
There are 2 types of similarity measures: –
-
Supervised similarity measure refers to the use of a supervised machine learning model to calculate how similar two items are. This model is trained on data that includes the correct answer, which it uses to learn how to predict the similarity of new items.
-
Manual similarity measure means calculating the similarity between two items using a predefined formula or method, without the use of a machine learning model. This approach is often used when it’s straightforward to calculate similarity, such as measuring the distance between two points in a space.
Here is a sample Python code for creating a similarity matrix:
from scipy.spatial.distance import cdist
# Calculate Euclidean distance between each sample and each cluster centroid
dist_matrix = cdist(X, kmeans.cluster_centers_)
# Create similarity matrix
similarity_matrix = 1/dist_matrix
# Print the similarity matrix
print(similarity_matrix)
"""
Output
array([[ 0.29246175, 7.074606 , 0.19764636],
[ 0.29424103, 2.23394674, 0.19550559],
[ 0.28016253, 2.3974543 , 0.18941707],
[ 0.29219179, 1.90353644, 0.1940395 ],
[ 0.28841184, 5.30147879, 0.19591195],
[ 0.31779005, 1.4770227 , 0.2136073 ],
"""
Each row in the similarity matrix corresponds to a sample, and each column corresponds to a cluster centroid. The higher the value in the similarity matrix, the closer the sample is to the corresponding cluster centroid.
Interpret results
The results of K-means clustering can be visualized using a scatter plot, as shown above. Each cluster is represented by a different colour, and the cluster centres are marked in red.
The results can also be evaluated quantitatively using various metrics such as inertia (sum of squared distances of samples to their closest cluster centre) and silhouette score (a measure of how close each sample in one cluster is to the samples in the neighbouring clusters).
from sklearn.metrics import silhouette_score
# Calculate silhouette score
sil_score = silhouette_score(X, labels)
# Print silhouette score
print('Silhouette Score: ', sil_score)
# Print inertia
print('Inertia: ', kmeans.inertia_)
# Inertia: 78.85144142614601
# Silhouette Score: 0.5528190123564095
In this code, kmeans.inertia_ returns the inertia of the KMeans clustering. A lower inertia means a better model.
In this code, silhouette_score(X, labels) calculates the silhouette score of the clustering result. A higher silhouette score indicates that the samples are well clustered.
That’s it for this blog. I hope you learned something useful about clustering ❤️❤️.



